Quiet Contempt

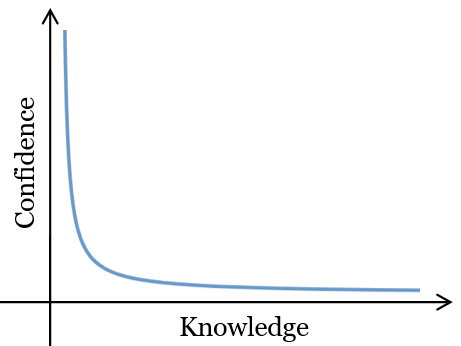
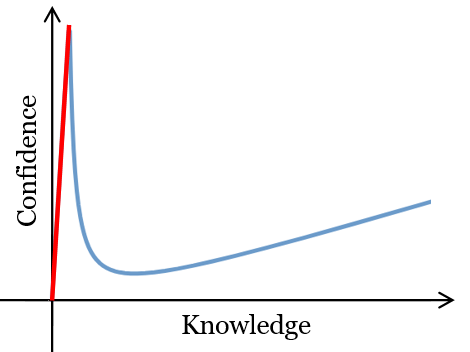
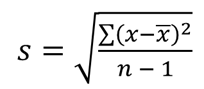Judging by the number of views at this blog, it seems like many of you already follow the suggestion of the above title.

But I really want you to ask yourself why you would listen to anything I say–or write, in this particular case–in the first place.

Now, it’s possible that you–for reasons beyond me–believe that I know what I’m talking about, and you come to read this blog in order to learn more.

It’s also possible that you believe that I don’t know what I’m talking about, but you still want to read something that might challenge your thinking. That’s not an unusual position at all; in fact, I find it rather admirable to do that. I find myself often reading things that I do not agree with; I find myself often actively looking for things that I do not agree with.

Why would I–or anyone else, for that matter–do that?

Well, some people are just looking for a fight. And, personally, I just don’t care about those kinds of people. They’re not reading to think; they’re reading to argue. They don’t ever engage in real conversation in that they only listen to others in order to craft a response rather than actually…you know…listening to those others.

Other people–and I’d put myself in this category–look for things that we disagree with specifically because reading those ideas makes me think about what I do believe. After all, how could I identify something is false without having some idea of what is actually true?

For example, as a math teacher, I’ve graded plenty of REALLY bad proofs. But I’ve also graded some proofs that were just a bit…”off.” There would be something in the argument that “just didn’t ring right.” It was often frustrating for me–and the student–to state that there was something wrong without knowing exactly what it was. Usually, I’d tell the student to give me a few minutes (or days) to think about it, and each time I was eventually able to pinpoint the error. Knowing and dwelling upon the correct answer gave me enough knowledge to eventually identify the incorrect parts of an incorrect answer.

But all of this has just been a long way to state that some people believe what I have to say, others don’t, and others haven’t really made up their minds yet.

But there’s actually another category of readers: those who realize that I sometimes know what I’m talking about.

And that’s the real catch. If I was always right, things would be easy: do what I say.

If I was always wrong, things would also be pretty easy: do the opposite of what I say. The inimitable Dwight from The Office best encapsulates this approach:

The problem is that I–and everyone else on earth for that matter–have the capacity to be both right and wrong about some idea.

Thus, the key question is not really “Who do you trust?” Let me make this strong claim: Trust is not binary. In other words, you cannot put people into simple “I trust this person” v. “I do not trust this person” categories.

I have a teenage son. You would think that Webster would define teenage son as “person you can not trust.” And there you would be wrong. I actually trust my teenage son quite a bit. For one thing, I absolutely trust him to make the wrong decision about nearly everything.* It is because of that nearly absolute trust that my wife and I have put certain safeguards in our home.

*And I don’t blame him one bit. It is almost the job description of a teenage boy to mess things up.

A much better question than “Who do you trust?” is “In what capacity can I trust someone?”

And by posing that question, I finally finish my 600-word introduction to the next few posts.

In my last post, I mentioned that there are two complementary scales that help us identify how we know something:

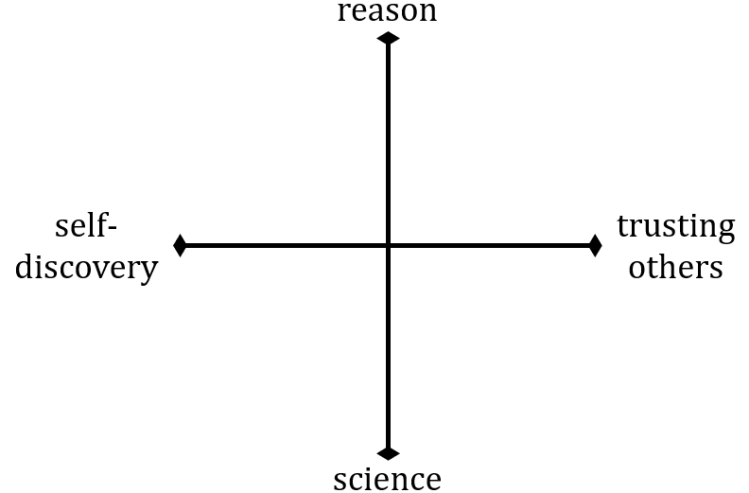
Starting with this post,* I want to examine first that horizontal scale: learning through self-discovery v. learning through our trust in others.

*And considering I’ve already burned nearly 650 words so far, I don’t expect to actually get very far this week.

And with that, let me go all the way back to the title of this post: Don’t Listen to Me. Well, you’ve made it this far, so you either (a) are terrible at instructions or (b) are expecting that the title was some sort of set-up. And, yes, it was some sort of set-up.

It is true that I do NOT want you to listen to me…about certain things…about many things…in fact, about most things.

Suppose you were to pick any topic at random. Well…you’re welcome because I just did. I googled “word of the day” and Merriam-Webster brought up the word encumber. I know what that word means, but–to be honest–the word encumber isn’t really that big of a topic. However, one of the definitions mentioned “to burden with a legal claim (such as a mortgage).” BINGO! Let’s talk about mortgages! (And that “whooshing” sound you hear now is my last reader leaving the site…)

I’ve had to go through the whole mortgage process before, signing 35 pages of the tiniest print imaginable. But I can’t say that I’m an expert on mortgages.

I’ve taught compound interest calculations in my mathematics classes before. But I can’t say that I’m an expert on mortgages.

I’ve even had the…privilege?…opportunity?…trauma?…of teaching how mortgage payments are calculated and how exactly pre-payments can cut time off of the payment schedule. BUT I CAN’T SAY THAT I’M AN EXPERT ON MORTGAGES.

I do know some of the above things, and I like to think that others could trust me on those aspects, but “Mortgages” as a topic is a LOT more than just calculating payments. For example, I don’t know the first thing about situations which would trigger a default and cause the bank to take my home. God–using other family members–has been good to my family, allowing us to always make the payments. And, frankly, I’m thrilled that I am unfamiliar with situations that would trigger a default.

So…long way back to this: Can you trust me when it comes to understanding mortgages? That’s a stupid question.

The better question is this: What things about mortgages can you trust me to know? Calculating a payment is about it.

But even then, you’ve only read my claims about those calculations. That actually takes us to the REAL question: How do you know that you can trust me for calculating a payment?

That’s for next week…

After spending far too long talking about being aware of how much we actually know about some topic, I am prepared to somehow get even more boring. It’s a gift, actually, to take something that is already mind-numbing and make it completely mind-deadening.

But the fact that you have pressed on and are now reading this sentence indicates* that you have a suitably dead soul, and we can press on. But don’t say you weren’t warned. This post is going to be packed full of Grade-A Boring. But I’m afraid that it’s all necessary for understanding the next few weeks’ posts.

*When first typing this sentence, I accidentally typed indicts. That might actually be a better description of the kind of person who reads/writes this stuff.

So…ask yourself the following:

How do we know anything at all in the first place?

I warned you at the end of my last post that this one was going to get philosophical, and few questions–if any–have gripped the minds of philosophers more than this one.

Naturally, the first thing a philosopher does is come up with a Big Name to describe this topic. This does two things:

1. It makes the the philosopher sound knowledgeable: the bigger the name, the bigger the brain.
2. It delays the need to actually answer the question. The effect is basically this: “I, [insert suitably ostentatious Greek name here] have founded the study of [insert newly-invented–but still suitably ostentatious–philosophical name here] and will be forever connected to this philosophical endeavor. It is up to you–the weak–to actually do the thinking.”

The “newly-invented–but still suitably ostentatious” term that some “suitably ostentatious Greek” settled upon was epistemology.

Now, I hate the way new terms are usually introduced: the word is given, followed by the definition. That might be an efficient way to give the information, but it is a horrible way to teach the information. Whenever I introduce a new term in my classes, the first thing I usually do is break down the work into its component parts.

One common example from my statistics classes is the term standard deviation. I usually give the term and then ask the students what is means. Of course, they look at me like I’m stupid (they’re not entirely wrong there…) because I’m the teacher and they’re the students: how could I expect them to know what the term means before I tell them?

Well, I hope by the time they reach a statistics class they have learned what the word standard means. Obviously, there are several definitions of the term, and I need to guide them to the one that is used in a statistics context. We eventually settle upon the idea that standard means something along the lines of “usual” or “typical.”

I also hope that they know what the word deviate means (while hoping that none of my students are one*)–basically, “to differ.”

*And, yes, I checked deviate v. deviant: https://brians.wsu.edu/2016/05/25/deviant-deviate/.

Thus, before we ever get to the definition of standard deviation, “we” (as if I really gave my students any choice) have settled upon “typical difference” as a basic description. It is then a “simple matter” of talking them through slightly more formal definition*:

*I think it was Malcolm Gladwell who quipped that every equation in a book cuts the number of readers in half. Then I guess I just lost two readers.

But enough of that boring side track as we now we return to our previous boring side track. The word epistemology is effectively two Greek words: episteme (“knowledge”) and logos (“logic; reason”). In other words, epistemology is the study of knowledge.

In particular, epistemology is the topic of our even more previous boring main track, asking this key question:

How do we know anything at all in the first place?

I’ve spent a lot of time thinking about how I’d address this because I usually find answers to this expressed along two different scales:

• personal discovery v. absolute trust in others

• pure reason v. scientific method*

*Especially here, I expect to take a lot of grief because a lot of people conflate these two ideas, but I will explain what is meant here over the next few weeks. No…wait…I don’t expect to take much grief at all. Grief can only come from readers. I’m guess I’m pretty safe then.

More times than you can count, I’ve gone back and forth on which these perspectives to use as we go forward in this blog.

Which perspective is the “right” one? They both certainly seem valid.

Which perspective is the “better” one? There are certainly pros and cons to each.

But the more I’ve thought through this problem, the more it became apparent that I couldn’t explain one of the scales without using the other. Perhaps the two scales are complementary rather than competitive.

Thus, I’ve come to believe that these two individual scales actually form a bit of a grid:

I suppose the approach that I’ve been taking for this blog asks the typical reader to be somewhere around here:

Why “leaning towards reason”? Well, I’ve asked you a lot to “think about it,” and then we’ve tried to reason ourselves towards some conclusion. Occasionally, however, I ask you to draw upon your own experiences–the observations that are the root of the scientific method.

Why “leaning towards trusting others”? That one’s pretty obvious: I’m asking you to trust me. But I also expect you to filter everything you read in the context of what you have already learned for yourself.

There’s certainly a biblical basis for this. The Bereans were famously commended in the book of Acts for both listening to Paul and Silas “with all readiness of mind,” but also “search[ing] the scriptures daily” to determine “whether those things were so” (Acts 17:11).

Now, keep in mind that all of this is only to discuss our knowledge of some truth. The truth itself is completely independent from our knowledge of it.

Isaac Newton famously discovered his Universal Law of Gravitation some 300-350 years ago (which has since been refined by Albert Einstein’s Theory of General Relativity), but I have a pretty good feeling that gravity–and the laws governing it–were around long before Newton.

But that’s just speculation…

So let’s finally finish this discussion of the Dunning-Kruger Effect.

Last week we looked at the slow and steady rise in the justified confidence someone develops as that someone slowly and steadily masters some discipline.

But let’s finish by looking at that initial spike.

If you think about it, this spike provides a good self-check on where one lies along the knowledge spectrum. How so? Well, if you’ve never had that soul-crushing drop that follows the spike, you’re likely on the very low end of the knowledge spectrum.

Let me give two examples from my own personal experience.

The first comes to my mind because of a conversation I recently had at lunch. The (thoroughly mind-numbing) topic was designing a survey questionnaire.

Now imagine that you were supposed to design some survey about any topic…say, the quality of the major news media outlets. Would you have said, in the words of the immortal Jeremy Clarkson,* “How hard could it be?”

*the most juvenile host out of the three fantastically juvenile (in other words…brilliant) hosts of the British Top Gear hosts–that is, the only real Top Gear

The novice quickly throws together some questions that on the surface appear to address the issue. Problem done!

If you’ve ever studied survey design (and, as part of some early graduate work, I was once stuck doing that very thing), you’ll quickly know that there are at least a half-dozen stages of properly designing a valid and reliable* survey. And several of these steps occur long before even writing a single question.

*By the time I finally give up on this blog, we will all be tired of these two terms. Why? They are everywhere when it comes to proper research designs. But, for now, don’t worry about what their specific meanings in the context of research.

“Aww…come on! You’re making it out to be harder than it really is!”

Anyone who uses that sentence, my friend, means that that person is stuck on the top of the spike: supremely confident but also supremely ignorant.

Consider even something as “simple” as asking about who people will vote for in some election. Consider–as an admittedly abridged example–that we tend to lump all candidates into the Republican or Democrat camps. There is a mammoth difference between the following two questions:

1. Do you plan to vote for the Democratic candidate or for the Republican candidate in the upcoming election?
2. Do you plan to vote for [insert the Democratic candidate’s actual name here] or for [Republican’s name] in the upcoming election?

Sure, there will likely be some overlap in the results of the two questions, but with a very partisan electorate, that overlap can make all of the difference.

The point here is not survey design (though it may come up at some point). The point is how you responded to the seemingly “simple” notion of designing a survey:

• The novice says, “How hard could it be?” out of sheer ignorance.
• The practiced amateur (such as a graduate student) says, “It’s really hard.”
• The seasoned professional says, “It is a hard task, but I’ve done it enough times that I think I’ve got a good handle on it.”

The problem is that we give the first answer while we think we’re giving the third one.

And THAT is where “soul-crushing doubt” serves as the proper self-check: If you have never had that soul-crushing doubt, then you have never moved past that spike of ignorant confidence.

And, you know…I originally planned to discuss two personal examples, but I think the one will suffice for now. Besides that other example is going to pop up indirectly time and time again over the next several weeks and months.

So…two good pieces of news!

1. short blog post this week!
2. done talking about Dunning-Kruger Effect!

Next week we will get a bit philosophical. But I’ll write about that next week. And–because I told you it will be philosophical–I suppose I’ll see you again in a few weeks…

So…in the last post, we saw this graph of the Dunning-Kruger Effect.* This week, I want to focus on the right side of the graph.

*I promise that we’re almost done with the DK Effect. I know it’s boring. I know I’M boring. But we always need to know where we really are on understanding some concept.

Malcolm Gladwell popularized the 10,000 Hour Rule in his book Outliers: The Story of Success. Gladwell makes no bones about it: this “rule” is more of a guideline than an absolute. But the principle that he promotes is that it takes about 10,000 hours of doing something to become a true expert.

Those who achieve 10,000 hours working on some concept are the ones at the extreme far right of that graph. And notice that these people have some rightfully-earned confidence in their understanding of that concept. Usually, that confidence has two aspects:

• a self-acknowledgement that they are genuinely good at that concept
  • example: a twenty-year car mechanic is justifiably confident in his ability to tackle just about any mechanical issue brought to his garage
• a self-acknowledgement that there are boundaries to that concept
  • example: that same mechanic understands that working on a large diesel engine (such as on a tractor-trailer) is a completely different thing

*Let me cite a personal example. My home A/C unit conked out one day, and I asked my friend to look at it. He handles immense building cooling systems that operate using chilled water technology. The first thing he said when he looked at my puny little home system was, “I’m not very familiar with these types.” The size of the system doesn’t matter; the type of technology does.

Obviously, there will be some overlap. Any car mechanic is going to be far better than me when it comes to large diesel engines simply because “car engine” and “tractor-trailer engine” both fall under the larger umbrella of “automotive mechanics.” But good mechanics in their fields are quite aware of the boundaries of their expertise.

Unfortunately, we “Average Joes” all-too-often act like “a mechanic is a mechanic is a mechanic.”

Without trying to evoke current affairs, we often act like “a doctor is a doctor is a doctor” because all (physician) doctors are somewhere under the large umbrella of “health care.” But there are huge differences from specialty to specialty. And [current affairs alert] there is a huge difference between a doctor who specializes in pharmaceuticals and a family physician who prescribes those medicines. Neither type of doctor is “more important” than the other. They are just different, and each type relies upon the other to fill in the knowledge gaps that they simply do have time to research for themselves.

But that is starting to get off topic, and I want to save what the word research means for a post all its own.

Returning to the task at hand, there is one aspect of this increased confidence that is especially important to a teacher. Now, you might say, “But I’m not a teacher.” Yes, you are.

We are all teachers.

Sure, some have teaching as a profession,* but everyone teaches at some point. You can’t be a parent without being a teacher. Even the very worst parents can’t help but teach their children something. Ask any person who was abandoned as a child, and they will tell you that their parents taught them something because of that abandonment–and usually none of it was good.

*I often tell my students this: “I am a professional teacher. That doesn’t mean that I’m any good. It just means that I get paid.”

But let’s consider professional teachers for the moment. And–humor me–I will do so by imagining everyone to be a professional teacher. This shouldn’t be that difficult. After the very least, just about all of us sat under some professional teacher at some point. We are just trying to put ourselves into their shoes for a bit.

First, ask yourself: “How did I end up teaching this material?”

The answer to that should be pretty obvious: you already had some innate talents in that area. After all, if you had no talent in that area, you’d never have developed any skills in that area. Also, keep in mind that most teachers tend to be fairly good at academics overall. So when, for example, a science teacher says, “I don’t have any talents in English,” what is usually meant is “I obviously have some talents in English; I’m just not proficient enough to teach it well.”*

*Ooo! Ooo! “Self-acknowledgement of boundaries!”

Thus, we arrive at the first application of the Dunning-Kruger Effect to teaching:

• A good teacher should be able to justifiably acknowledge his innate abilities in that subject.

But most of the students in the classroom do not share those innate abilities to the level of the teacher.

Obvious Qualifier 1: Many students do share those abilities, but they are the exceptions…not the rule.

Less Obvious Qualifier 2 (with a long explanation to go along with it…): As classes get more and more specific, the teachers also get more and more specialized. Thus, most people might consider college senior classes in mathematics to be highly specialized. Well, they are, but only relative to lower undergraduate-level (and certainly to high-school level) mathematics classes. Those who teach upper-level mathematics classes in college are usually much more specialized than the students in the classroom and have an innate talent in the specializations that the students in that room lack.

So what does this mean?

Well, let me go immediately to the second teaching application of the Dunning-Kruger Effect:

• A good chunk of the increased confidence among good teachers is mistakenly placed on the students.

Let me make this strong statement first: If a teacher thinks everyone in the class is an idiot, that’s a bad teacher.

To put it in different terms, a good teacher thinks that most of the students are capable of learning the material.* It’s just that a lot of the students have an insufficient background for immediate success: perhaps never having been taught how to truly study; perhaps lacking an adequate pre-requisite course; etc.

*It should be obvious that not everyone can learn everything. We all have different innate academic strengths and weaknesses that need identified and developed just as much as we all have different innate physical strengths and weaknesses that need identified and developed.

The issue that good teachers face is failing to recognize that the teacher’s innate abilities in the material make it appear easier to learn that material than it really is. In other words, teachers are sometimes embarrassed to teach the basics in some subject because–once that teacher first learned the concept–it looked painfully obvious in retrospect.

Now, I make no claims about being a good teacher. But let me conclude this post with a personal example.

For years, I had the privilege of teaching a beginning statistics course. The real “fun” in that course doesn’t really kick in until the end when discussing tests of significance and regression. But to get there, we had to wade through the basic topics of standard deviation and probability.

The first several years that I taught these beginning topics, I was basically embarrassed to teach them. My thinking was basically this: “These are college students. They are probably bored out of their minds with these easy items.” Indeed, they were bored out of their minds, but it wasn’t because of the ease of the material. (I’ll let you discern the reason…)

But I was subsequently puzzled at the low grades on their tests…until it finally dawned on me. There were two reasons they were getting poor grades.

1. The material was tougher to them than I realized.
2. I had taught it poorly because I assumed they already knew it.

I don’t claim to be genuinely good at statistics. But compared to what I do know, those beginning concepts like standard deviation and probability seem obvious.

I failed my students because, as I learned more and more, my confidence in statistics justifiably increased, but I had misplaced that confidence. I unfairly attributed to the students an ability in statistics that they just did not have.

It was doubly unfair in that their very presence in the room was a tacit admission that they were not experts in the material.

And let that be my warning to all teachers: If a student chooses (or, more likely, his parents choose for him) to honor you with his presence in your classroom, there is a silent admission from that student that he does not yet know the material. Repay that honor by assuming that he genuinely does not know that material and teach him the material; don’t just assume its obvious–because to him it is not.

Let me briefly review the Dunning-Kruger Effect: the more that you know about some topic, the less confidence you have that you have mastered that topic. Effectively, as knowledge goes up, confidence goes down. But more “fun” (and by “fun,” I mean that it better affords me the opportunity to ridicule the stupid) is that as knowledge goes down, confidence goes up.

If we were to visualize that statement as a graph, it would look something like this:

Now, that description is a bit of an over-simplification of Dunning and Kruger’s findings, but it does get the major point across fairly well.

The Dunning-Kruger Effect is actually a more nuanced, however, and a more accurate graph of this effect would look like this:

This seems to line up a bit more accurately with our educational experiences. If you recall, I opened up my last post with my stereotyped view of college undergraduates. Indeed, most freshmen do enter college with very little knowledge (of their chosen majors, that is) and very little confidence either.

But as those freshmen proceed through those introductory courses and become sophomores, their confidence in their abilities (especially when they compare themselves to new incoming freshmen) rockets at a pace far faster than what their increased knowledge really permits. This is illustrated portion shown in red below:

Fortunately, college is a (at least) four year process, and the Junior Year comes riding in alongside its better-known accomplices of Pestilence, War, Famine, and Death.

The college junior is at once both a beautiful and terrible thing. Beautiful in that the student is now more open and receptive to his teachers than ever before. Terrible in that the student is…well…have you ever really seen a more pitiful sight than a college junior?

Just as rapidly as the early confidence rose, it evaporates. I remember that taking place in my own college career. There was a certain emptiness that crept in as I realized that, for every one thing that I learned about some topic, I was made aware of ten more things about that topic that I never even knew existed. As I learned more and more, I realized that there was much more and much more yet to learn.

But here is where people tend to misapply the Dunning-Kruger Effect. Note that as you or I learn more, “less confidence” does not mean that we know less. That idea (“knowing more” = “knowing less”) is an obvious contradiction. What it does mean is that we become less and less confident that we have genuinely mastered the entire concept.

Another misconception of the Dunning-Kruger Effect is the belief that learning more and more undermines our existing knowledge. Let me illustrate by going back to the “kindergartners learning addition” example from my last post. Imagine that the squares below indicate how much these children know about basic addition: the darker the square, the more they have learned.

These students objectively know more and more about basic addition. Even better, they can and should have more and more confidence in their ability to conduct such basic addition.

However, as they learn more and more basic addition, these kindergartners should become more and more aware of other types of arithmetic: subtraction, multiplication, division. See image below:

As their knowledge objectively increases, they become more and more aware that the mathematical “world” is far larger than just that small “world” of addition.

As students master arithmetic, they then are made aware of the larger mathematical worlds of algebra…then trigonometry…then calculus…then ad infinitum…

Thus, as one’s mathematical knowledge increases, his confidence in his mastery of “Mathematics” erodes considerably. Of course, I am grateful for the mathematics that I have had the privilege to learn and to teach, but all of that learning has made me better appreciate how much there actually is out there mathematically.

In fact, it made me finally appreciate what my high school basketball coach* told us in practice. Being high school students, we had reached peak “know it all” attitude. What could this guy actually teach us?!? One day, he had (legitimately) had enough and remarked, “I’ve forgotten more basketball than you will ever learn.” We thought that a ridiculous exaggeration.

*Yes, I “played” high school basketball. I went to a small Christian school in which try-outs consisted of checking for a steady pulse.

You know what? Having taken a lot of mathematics over the years, I now know what he meant. Indeed, I have forgotten more mathematics over the years than most of my students will even learn.* But I also appreciate the humility in which that statement can be made. My coach didn’t make that comment smugly (though I’ll admit that we needed put into our place) but rather as just a statement of fact.

*Yes, there are exceptions. One of them has earned his PhD, conducted post-doc work in England, and would easily blow me away with his knowledge. Fortunately, he’s just about the nicest guy on the planet and would just use that as an opportunity to help me grow in my own knowledge.

There is just sooooooo much out there to learn, and I save my Quiet Contempt for those who enroll at Facebook Mom University* and think they know everything.

*Sure, “The Left can’t meme,” but Church Mom is even worse.

In the next post, I plan to begin looking at the right side of the Dunning-Kruger curve and point out what its slow and steady rise means.

From teaching undergraduates, I’ve come to believe the following:

• As a freshman, you get overwhelmed by the simple.
• As a sophomore, you think you know everything.
• As a junior, you think you know nothing.
• As a senior, you don’t care what you know.

But, as the Preacher reminds us, “there is no new thing under the sun” (Eccles. 1:9b). Meaning…? I guess my belief above wasn’t as original as I’d hoped.

In 1999, Cornell psychologists David Dunning and Justin Kruger described a rather interesting pattern in human thinking. They conducted experiments showing that, essentially, as someone learned more and more about some topic, he would become more and more aware of just how much there was to learn about that topic and, consequently, became more and more aware of how little he actually knew in relation to the entirety of that topic. This phenomenon became known as the “Dunning-Kruger Effect.”

In essence: knowledge up –> confidence down.

But a much more “fun” part of Dunning and Kruger’s findings is that the inverse also holds: knowledge down –> confidence up. In other words, the less that someone knew about some topic, the more he thought that he knew.

Once you really think about it, it just makes sense.* The smaller some “world,” the less there is to know about that world.

*I know…I know…”making sense” doesn’t prove anything. But Dunning and Kruger have experimental evidence to support the idea.

Consider a kindergartner who is just learning basic addition: 1 + 1 = 2, 2 + 3 = 5, etc. To that child, the whole “world” of mathematics is just that simple addition. To that child, “mathematics” equals “simple addition.” To that child, mastering that little bit of addition means having mastered mathematics. That child literally thinks that he knows everything there is to know about mathematics. Why? Because he knows everything there is to know about what he perceives is mathematics.

Of course, the child soon gets into subtraction, multiplication, and division, and that child soon realizes that the “world” of mathematics is bigger than he originally thought.

But, even then, the actual world of mathematics is far, far bigger than he can possibly conceive. It is not unusual for a child to ask me what it means to be a mathematician: “Do you multiply really big numbers?”*

“No, you sweet innocent…no. I usually just cry myself to sleep wondering if I’ll ever nail down that proof of the Third Sylow Theorem.”

To be honest, the more I learned about math, the more I learned that I was hopelessly lost if I wanted to learn everything there is to know about mathematics–even learning about something as “simple” as multiplication. Borrowing from my example above, the seemingly simple “world of multiplication” is far larger than you or I could possibly imagine.

To get a sense of this, I invite you to visit the https://mathworld.wolfram.com/ website (I know you won’t, but you’re still invited…), and plug the word product into the search bar. You will get 91 pages of results. Page 1 alone lists links to the following:

• dot product (very familiar to those studying vectors)
• inner product (ditto)
• Cartesian product (familiar to those beginning to study sets)
• direct product (familiar to those studying abstract algebra)
• Jordan product (ditto)
• cup product (“Huh?”)
• Hadamard product (“OK, now you’re just making stuff up.” “Am not!” “Are, too!” “Am not!”…)

And that’s just the first page…out of ninety-one…just dealing with multiplication!

Consider your own line of work. Don’t you get a slight, sly–and certainly irritated–smile when someone else mentions how easy your job is?* Of course you do because you know that there are 100 things about your job that the other person doesn’t know…and probably doesn’t even know that they exist.

*Either that, or you want to punch him square in the face. But this blog is called Quiet Contempt, so we’ll keep it to just the sly smile.

The whole point is that we all need to develop an awareness that we don’t know everything…especially if we are just beginning to study the topic (or, far worse, if all of our “study” is reading posts from our isolated bubble of social media friends).

Even the Bible makes a big deal out of this very thing. In I Timothy 3, Paul lays out the qualifications for a pastor (a “bishop”). In verse 6, the given requirement is “Not a novice, lest being lifted up with pride he fall into the condemnation of the devil.” The prospective pastor is expected to spend a great deal of time transforming from a “novice” in the faith to one with much more maturity.

Paul himself sat at the feet of Jewish masters for years. However, once he was saved on the road to Damascus, he recognized that he was still a “novice” Christian even though he was highly experienced in Judaism. In Galatians 2:1 (see chapter 1 for context), Paul notes that he spent some 14 years in private study before moving into his public ministry.

In my next post, we will take a slightly deeper look into the Dunning-Kruger Effect and see what it means as we slowly but steadily learn more and more about different topics.

But, to conclude, let me return to my starting illustration and show how the Dunning-Kruger Effect neatly describes my observations about undergraduates:

• Freshman are typically in awe as they are introduced to the basic concepts of their chosen majors. But, being basic, those concepts aren’t typically too difficult to grasp, leading to…
• Sophomores that think they have a pretty good handle on their major (and college life in general). But this is when they usually take their first deep, year-long courses. Thus, especially in the second semester, they begin to realize that there’s a LOT more our there than they possibly imagined, leading to…
• Juniors that come to realize that learning everything about their major is futile. Often, their second deep, year-long courses go even deeper, and they realize that the rabbit hole doesn’t just keep getting deeper and deeper–it drops all the way to Wonderland. (For the record, juniors are often my favorite students. They’ve learned enough to speak knowledgeably about their majors, but have a healthy respect for just how much their majors entail.) This finally leads to…
• Seniors that just want to finish. They probably still have a love for their major (though it is a far more mature and respectful love than that shown by eager freshmen) and still want to learn more about it, but they are just too burned out on formal learning and are just wanting to begin to apply what they now know is a just a fraction of what their major really holds in store.

…

…

…

…

Then come graduate students…

So…why start this blog? What could I possibly say that hasn’t been stated time and again already?

Well, I’m in my mid-40s. I’ve never kept a diary. I’ve never really committed my thoughts to paper (or electrons, in this case). I think that I have a good deal to say, and I think that all of us (myself foremost) have a good deal to hear.

But I’m not suggesting that I’m writing for others to read; instead, I’m writing for me to speak. (If you want to queue up a “If a tree falls…” joke here, go for it. I’ve certainly made it easy enough for you.) Your reading it is just a bonus to me.

The title of this blog should clue you in as to my main motivation for finally writing. I’ve had the privilege of a lot of education and, thanks to my parents and some key friends and colleagues, I’ve even had the privilege of learning. Virtually everything I know has been because—to ape Newton—I’ve “stood upon the shoulders of giants.”

One thing in particular that I have had the privilege of learning has been research methodology. Even better, I’ve had the privilege of teaching research methodology. And if there’s one thing that Facebook and Twitter have taught me, it’s that people have no idea how research works.

Over the last few years, I’ve privately seethed as I’ve read the relentless parade of stupid through social media. I’ve had a…well…“quiet contempt,” if you will.

One of my favorite passages in Scripture recounts Jesus’ driving the money changers from the temple. One prevailing narrative describes Jesus’ “righteous anger.” Well, of course He was angry. John records that His actions reminded the disciples that “it was written, The zeal of thine house hath eaten me up” (John 2:17).

But I find another phrase earlier in the story to be quite enlightening. In verse 15, John writes, “And when he had made a scourge of small cords…” In other words, the Divine Example basically sat down and took His time preparing His response to the situation. So…was Jesus angry? Yes. Was He in an uncontrollable rage? Absolutely not.

My prayer is that that theme will remain throughout this blog. While I doubt I’ll ever physically—or even proverbially—use a whip, I hope to spend all my time preparing it. But keep in mind that I intend for it to remain my “whip.” By that, I mean that I hope no one ever uses what I write to try to browbeat others. It is intended only for the education of the reader. Frankly, it is also for my own education. As a teacher, I’ve learned so well the adage that you will never understand anything so well as when you try to explain it for yourself. Thus, my feeble attempts to put my feeble thoughts into feeble words is mostly for me to organize for myself the myriad of ideas spinning around in my head. Having others read what I write gives me added incentive to get it correct as best as I can.

And thus we get to the end of this introduction. Why am I writing? For me. To help me put my thoughts into words and hopefully to leave some of what I’ve acquired over the years to my kids and their eventual families. If you choose to join me on this personal journey of mine, I’m glad to have you along. If you don’t join me, does that really change anything? Of course not. It’s not as if you’d read anything of mine before anyway. Besides, there are likely far safer places to explore than what is going on in my head.